<백준 10872번 - 팩토리얼> https://www.acmicpc.net/problem/10872
○문제
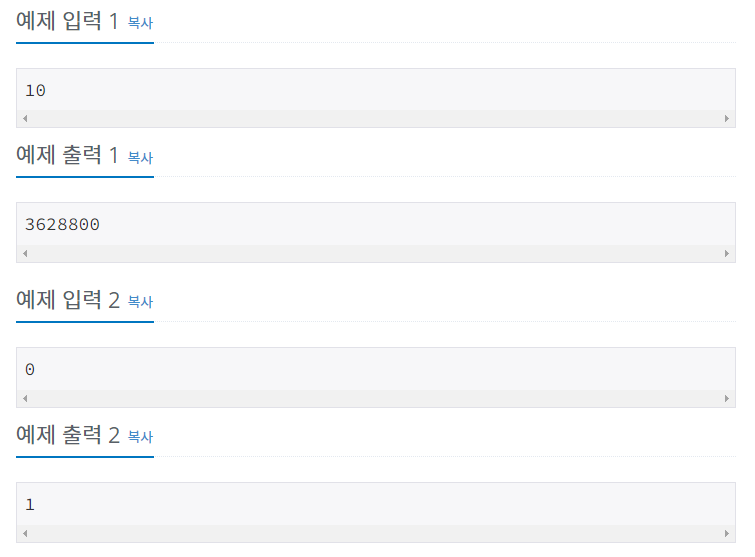
0보다 크거나 같은 정수 N이 주어진다. 이때, N!을 출력하는 프로그램을 작성하시오.
○입력
첫째 줄에 정수 N(0 ≤ N ≤ 12)이 주어진다.
○출력
첫째 줄에 N!을 출력한다.
import sys
n = int(sys.stdin.readline())
def factorial(n) :
if (n > 1) :
return n * factorial(n-1)
else :
return 1
print(factorial(n))<백준 10870번 - 피보나치 수 5> https://www.acmicpc.net/problem/10870
○문제
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.
이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다.
n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
○입력
첫째 줄에 n이 주어진다. n은 20보다 작거나 같은 자연수 또는 0이다.
○출력
첫째 줄에 n번째 피보나치 수를 출력한다.

import sys
n = int(sys.stdin.readline())
def fib(n) :
if n >= 2 :
return fib(n-1) + fib(n-2)
if n == 1 :
return 1
if n == 0 :
return 0
print(fib(n))
- 오류: 0번째를 포함하지 않고 작성하였다.
def fib(n) :
if n > 2 :
return fib(n-1) + fib(n-2)
else:
return 2
~ 수정:
def fib(n) :
if n >= 2 :
return fib(n-1) + fib(n-2)
if n == 1 :
return 1
if n == 0 :
return 0
<백준 25501번 - 재귀의 귀재> https://www.acmicpc.net/problem/25501
○문제
정휘는 후배들이 재귀 함수를 잘 다루는 재귀의 귀재인지 알아보기 위해 재귀 함수와 관련된 문제를 출제하기로 했다.
팰린드롬이란, 앞에서부터 읽었을 때와 뒤에서부터 읽었을 때가 같은 문자열을 말한다. 팰린드롬의 예시로 AAA, ABBA, ABABA 등이 있고, 팰린드롬이 아닌 문자열의 예시로 ABCA, PALINDROME 등이 있다.
어떤 문자열이 팰린드롬인지 판별하는 문제는 재귀 함수를 이용해 쉽게 해결할 수 있다. 아래 코드의 isPalindrome 함수는 주어진 문자열이 팰린드롬이면 1, 팰린드롬이 아니면 0을 반환하는 함수다.
def recursion(s, l, r):
if l >= r: return 1
elif s[l] != s[r]: return 0
else: return recursion(s, l+1, r-1)
def isPalindrome(s):
return recursion(s, 0, len(s)-1)
print('ABBA:', isPalindrome('ABBA'))
print('ABC:', isPalindrome('ABC'))
정휘는 위에 작성된 isPalindrome 함수를 이용하여 어떤 문자열이 팰린드롬인지 여부를 판단하려고 한다.
구체적으로는, 문자열 S를 isPalindrome 함수의 인자로 전달하여 팰린드롬 여부를 반환값으로 알아낼 것이다. 더불어 판별하는 과정에서 recursion 함수를 몇 번 호출하는지 셀 것이다.
정휘를 따라 여러분도 함수의 반환값과 recursion 함수의 호출 횟수를 구해보자.
○입력
첫째 줄에 테스트케이스의 개수 T가 주어진다. (1≤T≤1000)
둘째 줄부터 T개의 줄에 알파벳 대문자로 구성된 문자열 S가 주어진다. (1≤|S|≤1000)
○출력
각 테스트케이스마다, isPalindrome 함수의 반환값과 recursion 함수의 호출 횟수를 한 줄에 공백으로 구분하여 출력한다.

import sys
t = int(sys.stdin.readline())
def recursion(s, l, r) :
if l >= r:
return 1 #한 글자면 무조건 팰린드롬
elif s[l] != s[r]: return 0 #제일 앞글자와 제일 뒷글자가 같지 않으면 팰린드롬 x
else:
recursion_num[l+1] = 1
return recursion(s, l+1, r-1)
def isPalindrome(s):
recursion_num[0] = 1
return recursion(s, 0, len(s)-1)
for i in range(t):
s = sys.stdin.readline().rstrip()
recursion_num = [0]*len(s)
print(isPalindrome(s), recursion_num.count(1))
- 오류1: 리스트를 생성할 코드 위치
t = int(sys.stdin.readline())
recursion_num = [0]*t
~ 수정1:
for i in range(t):
s = sys.stdin.readline().rstrip()
recursion_num = [0]*t
print(isPalindrome(s), recursion_num.count(1))
- 오류2: recursion_num = [0]*t
리스트의 크기를 t만큼이 아니라, 문자열의 길이만큼 주어야 한다.
~ 수정2: recursion_num = [0]*len(s)
<백준 24060번 - 알고리즘 수업 - 병합 정렬1> https://www.acmicpc.net/problem/24060
○문제
오늘도 서준이는 병합 정렬 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자.
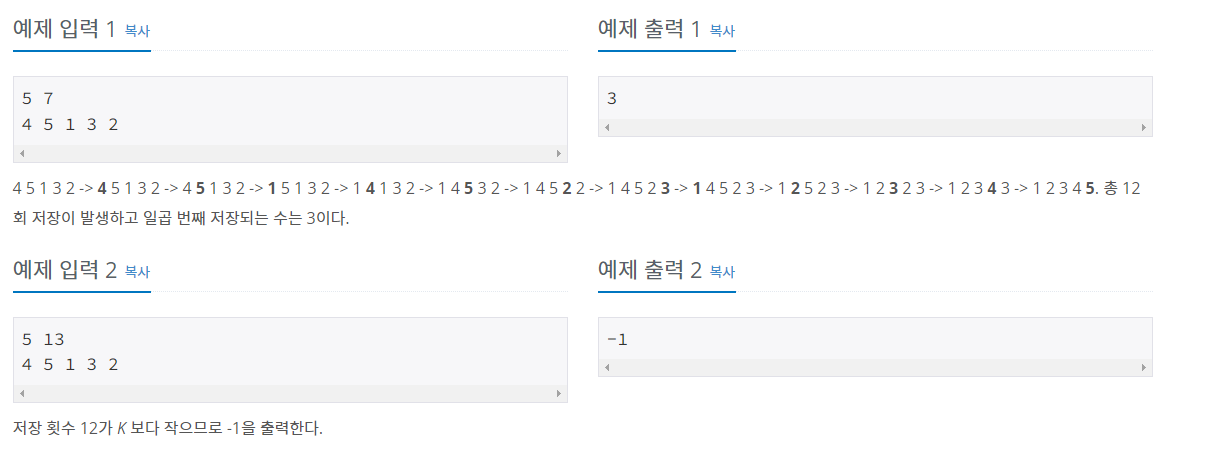
N개의 서로 다른 양의 정수가 저장된 배열 A가 있다. 병합 정렬로 배열 A를 오름차순 정렬할 경우 배열 A에 K 번째 저장되는 수를 구해서 우리 서준이를 도와주자.
크기가 N인 배열에 대한 병합 정렬 의사 코드는 다음과 같다.
merge_sort(A[p..r]) { # A[p..r]을 오름차순 정렬한다.
if (p < r) then {
q <- ⌊(p + r) / 2⌋; # q는 p, r의 중간 지점
merge_sort(A, p, q); # 전반부 정렬
merge_sort(A, q + 1, r); # 후반부 정렬
merge(A, p, q, r); # 병합
}
}
# A[p..q]와 A[q+1..r]을 병합하여 A[p..r]을 오름차순 정렬된 상태로 만든다.
# A[p..q]와 A[q+1..r]은 이미 오름차순으로 정렬되어 있다.
merge(A[], p, q, r) {
i <- p; j <- q + 1; t <- 1;
while (i ≤ q and j ≤ r) {
if (A[i] ≤ A[j])
then tmp[t++] <- A[i++]; # tmp[t] <- A[i]; t++; i++;
else tmp[t++] <- A[j++]; # tmp[t] <- A[j]; t++; j++;
}
while (i ≤ q) # 왼쪽 배열 부분이 남은 경우
tmp[t++] <- A[i++];
while (j ≤ r) # 오른쪽 배열 부분이 남은 경우
tmp[t++] <- A[j++];
i <- p; t <- 1;
while (i ≤ r) # 결과를 A[p..r]에 저장
A[i++] <- tmp[t++];
}
○입력
첫째 줄에 배열 A의 크기 N(5 ≤ N ≤ 500,000), 저장 횟수 K(1 ≤ K ≤ 108)가 주어진다.
다음 줄에 서로 다른 배열 A의 원소 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 109)
○출력
배열 A에 K 번째 저장 되는 수를 출력한다. 저장 횟수가 K 보다 작으면 -1을 출력한다.
import sys
def merge_sort(list):
if len(list) == 1:
return list
mid = (len(list)+1)//2
left = merge_sort(list[:mid])
right = merge_sort(list[mid:])
print(left)
print(right)
i,j = 0,0
list2 = []
while i < len(left) and j < len(right):
if left[i] < right[j]:
list2.append(left[i])
cnt.append(left[i])
i+=1
else:
list2.append(right[j])
cnt.append(right[j])
j+=1
while i < len(left):
list2.append(left[i])
cnt.append(left[i])
i+=1
while j < len(right):
list2.append(right[j])
cnt.append(right[j])
j+=1
return list2
n, k = map(int,sys.stdin.readline().split())
a = list(map(int,sys.stdin.readline().split()))
cnt = []
merge_sort(a)
if len(cnt) >= k:
print(cnt[k-1])
else:
print(-1)<백준 2447번 - 별찍기 -10> https://www.acmicpc.net/problem/2447
○문제
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다.
크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다.
***
* *
***
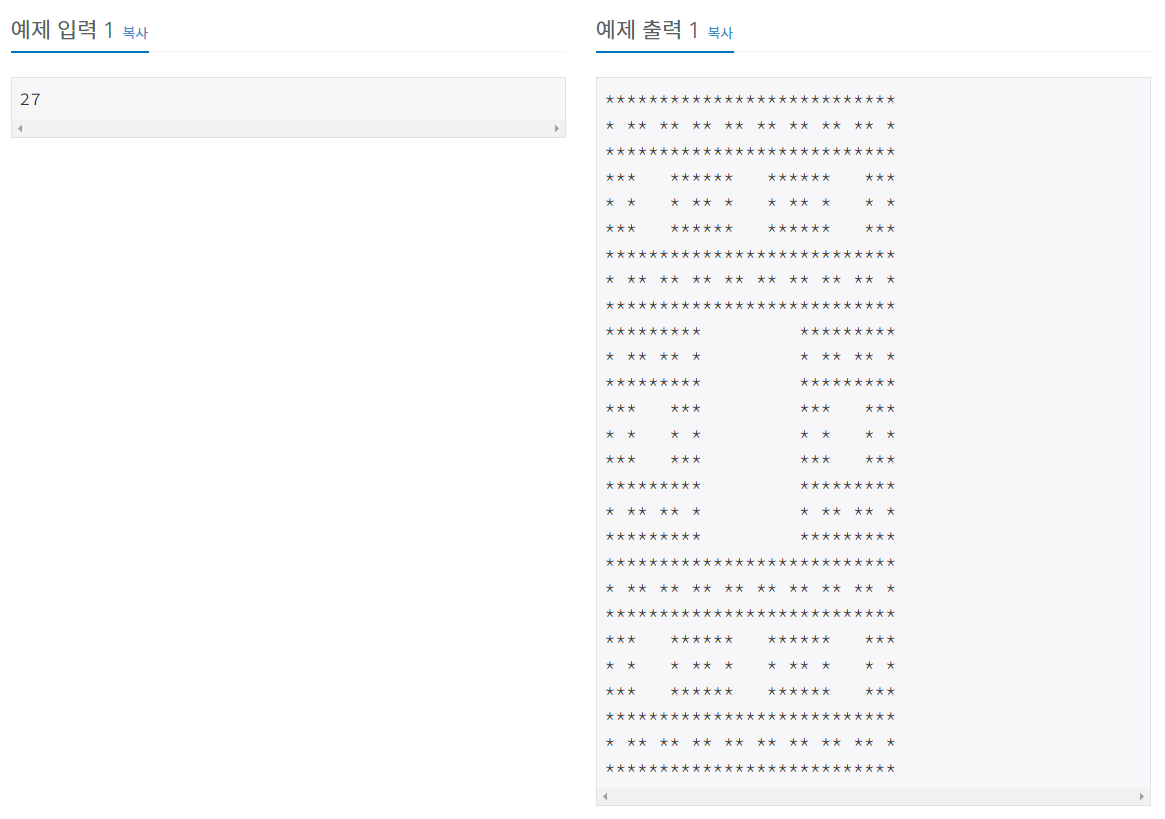
N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다. 예를 들어 크기 27의 패턴은 예제 출력 1과 같다.
○입력
첫째 줄에 N이 주어진다. N은 3의 거듭제곱이다. 즉 어떤 정수 k에 대해 N=3k이며, 이때 1 ≤ k < 8이다.
○출력
첫째 줄부터 N번째 줄까지 별을 출력한다.
import sys
sys.setrecursionlimit(10**7)
n = int(sys.stdin.readline())
def star(n):
if n == 3:
return ['***','* *','***']
if n > 3:
arr = star(n//3)
stars = []
for i in arr:
stars.append(i*3)
for i in arr:
stars.append(i+' '*(n//3)+i)
for i in arr:
stars.append(i*3)
return stars
print('\n'.join(star(n)))
- 리스트 함수 ''.join()을 새로 배웠다.
<백준 11729번 - 하노이 탑 이동 순서> https://www.acmicpc.net/problem/2447
○문제
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다.
크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다.
***
* *
***
N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다. 예를 들어 크기 27의 패턴은 예제 출력 1과 같다.
○입력
첫째 줄에 N이 주어진다. N은 3의 거듭제곱이다. 즉 어떤 정수 k에 대해 N=3k이며, 이때 1 ≤ k < 8이다.
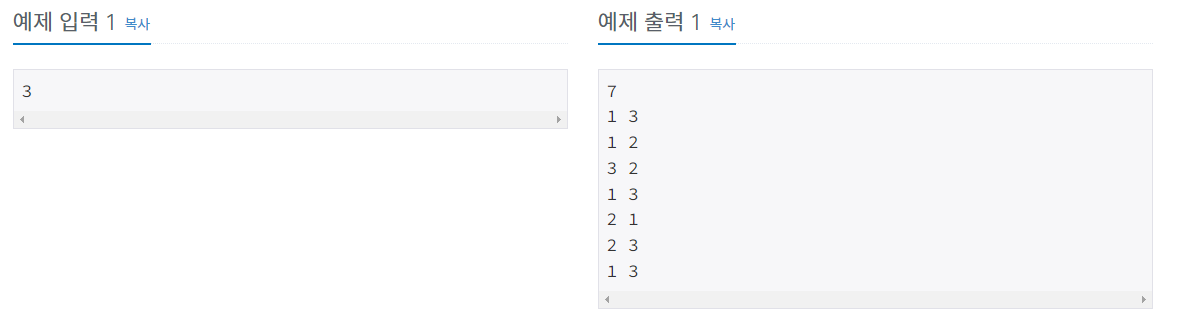
○출력
첫째 줄부터 N번째 줄까지 별을 출력한다.
import sys
sys.setrecursionlimit(10**7)
n = int(sys.stdin.readline())
def hanoi_tower(n, from_bar, to_bar) :
if n == 1 :
print(from_bar, to_bar)
else:
hanoi_tower(n-1, from_bar, 6-from_bar-to_bar)
print(from_bar, to_bar)
hanoi_tower(n-1, 6-from_bar-to_bar, to_bar)
print(2**n-1)
hanoi_tower(n, 1, 3)
하노이 탑 이동 횟수 공식: 2**n-1
'파이썬(PYTHON) > 코딩테스트' 카테고리의 다른 글
| 백준 단계별 - 집합과 맵 (1) | 2022.10.08 |
|---|---|
| 백준 단계별 - 브루트 포스 (0) | 2022.10.02 |
| 백준 단계별 - 정렬 (0) | 2022.09.25 |
| 백준 단계별 - 문자열 (0) | 2022.09.08 |
| 백준 단계별 - 함수 (0) | 2022.09.04 |



